[Ghoser777]

I know this is the perfect place to post for peer review of a mathematical question based on the previous thread

One of my fellow math teachers posed a question that none of us had an answer to initially, and it took me about a month to formalize what I'm about to show you. It essentially says, given a parallelogram and 2 of the angles formed by drawing the diagonals, what are the possible solutions for another of the diagonal angles. In the document I'm linking to, the original question (which I generalized), was if angles b and d are given, what are the possible measures of c? There are 6 possibilities for givens, and I believe I addressed them all in adequate detail. It's kind of interesting that the first 2 cases do not define unique solutions (there are 2), while the last four do define unique solutions.

Feed back welcome!

http://homepage.mac.com/fahrenba/pda.pdf

[Ghoser777]

:crickets:

[turtle777]

Originally Posted by Ghoser777

I know this is the perfect place to post for peer review of a mathematical question based on the previous thread

You got it.

/got nothing
//nothing at all

[f1000]

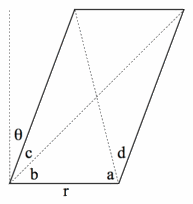
For any given parallelogram, θ and r represent the skew and the ratio of the base to the height, respectively. We can define the diagonal angles in terms of θ and r as follows:

a = acot[r-tan(θ)]*
b = acot[r+tan(θ)]
c = atan[r+tan(θ)]-θ
d = atan[r-tan(θ)]+θ

From any pair of {a, b, c, d}, we can determine θ and r and thereby derive the remaining diagonal angles.

For {a, b},

θ = atan[0.5[cot(b)-cot(a)]]
r = 0.5[cot(b)+cot(a)]

For {a, d},

θ = a+d-π/2
r = cot(a)-cot(a+d)

For {b, c},

θ = π/2-(b+c)
r = cot(b)-cot(b+c)

For {a, c},

2tan(c)tan(θ)^2+[cot(a)tan(c)-1]tan(θ)+[tan(c)+cot(a)] = 0
Two real roots, which I assume lead to the interchangeability of {b, d}

For {b, d},

2tan(d)tan(θ)^2+[1-cot(b)tan(d)]tan(θ)+[tan(d)-cot(b)] = 0
Two real roots, which I assume lead to the interchangeability of {a, c}

For {c, d},

By transposing variables used in the proof for {a, b},

a = atan[r-tan(θ)]+θ
b = atan[r+tan(θ)]-θ

θ = atan[0.5[cot(c)-cot(d)]]
r = 0.5[cot(c)+cot(d)]

*For negative values of a, add π.

NOTE: There should be some way to simplify the two second order cases, but I'm having trouble seeing it.

[f1000]

Originally Posted by Ghoser777

Feed back welcome!

http://homepage.mac.com/fahrenba/pda.pdf

1. In solution 3b, there seems to be a typo.
2. The proof for set {a,d} seems to be missing.
3. This sentence bothers me: ...the values of a and c may be interchanged. While it's true that properties 1 & 2 remain invariant when you swap a with c, it's not true that a and c are interchangeable given a particular set of b and d. I guess I don't see the point to this observation.
4. I am looking over your trigonometric identities, but I'm not double-checking your calcs because I assume you've already done so with a math package. From my cursory examination, your proof makes sense.
5. Your symmetry trick turned my 3rd order nightmare into a simple proof!

[Rolling Bones]

OK.
?¿?

[Ghoser777]

In solution 3b, there seems to be a typo.

Fixed

The proof for set {a,d} seems to be missing.

I'm not sure if I follow. The case is not different up to isomorphism - just a relabeling gives the exact same type of problem.

[*]This sentence bothers me: ...the values of a and c may be interchanged. While it's true that properties 1 & 2 remain invariant when you swap a with c, it's not true that a and c are interchangeable given a particular set of b and d. I guess I don't see the point to this observation.

Of course its true - given b and d, there are two interchangeable solutions for a and c. What that means is, if you have a parallelogram with a given b and d, and c comes out to be 30 and a comes out to be 50, then there exists another parallelogram with the same b and d values where a is 30 and c is 50. If you have GSP, you can convince yourself of this fact fairly quickly.

I
am looking over your trigonometric identities, but I'm not double-checking your calcs because I assume you've already done so with a math package. From my cursory examination, your proof makes sense.

Nope, did it all by hand! I did use GSP to double check that my algorithms worked.

Your symmetry trick turned my 3rd order nightmare into a simple proof!

Glad I could help.

[f1000]

Originally Posted by Ghoser777

I'm not sure if I follow. The case is not different up to isomorphism - just a relabeling gives the exact same type of problem.

Indeed, but I thought that you would mention this explicitly for your students.

Originally Posted by Ghoser777

Of course its true - given b and d, there are two interchangeable solutions for a and c. What that means is, if you have a parallelogram with a given b and d, and c comes out to be 30 and a comes out to be 50, then there exists another parallelogram with the same b and d values where a is 30 and c is 50. If you have GSP, you can convince yourself of this fact fairly quickly.

Give me a few minutes to think about this.

Originally Posted by Ghoser777

Nope, did it all by hand! I did use GSP to double check that my algorithms worked.

As you can see, I'm quite a bit lazier than you.

[DayLateDon]

Hello ...

Ghoser, you cannot go from "cos(this) = that" to "this = arccos(that)"!
(Why hasn't anyone else pointed this out?)

In Solution 1a, the following equations (the first one is yours)

Eq1: cos( 2c+b+d ) = cos(b+d) - 2 sin(b) sin(d)
Eq2: cos( 2a+b+d ) = cos(b+d) - 2 sin(b) sin(d)

are simultaneously true. To see why, recall a+b+c+d = pi,
and manipulate as follows:

cos( 2c+b+d ) = cos( 2pi - (2c+b+d) )
= cos( 2(a+b+c+d) - (2c+b+d) )
= cos( 2a+b+d )

If "arccos-ing" both sides were legal, then one consequence
of applying that process to Eq1 and Eq2 would be that "a"
always equals "c". (Likewise, via a separate pair of
substitutions, "b" always equals "d".) Clearly, this is not
true.

The proper conclusion turns out to be that "2a+b+d" and
"2c+b+d" account for the _two_ values of "T" (in the range
0 to 2pi) satisfying

cos(T) = cos(b+d) - 2 sin(b) sin(d) <-- call that "X"

Note that the range 0 to 2pi needs justification as well, but it's
pretty straightforward.

As a result, we get these two cases:

1. 2a + b + d = arccos(X) and 2c + b + d = 2pi - arccos(X)

2. 2c + b + d = arccos(X) and 2a + b + d = 2pi - arccos(X)

(You effectively make this observation at the end of your
Solution 1a, but unfortunately that observation is undermined
by the flawed derivation.)

Now, if we suspected that the result should be unique (as with
the other cases), we should check whether the geometry of the
situation at hand makes one of the symbolic calculations
extraneous. It doesn't: We can build a parallelogram with
a = pi/2 (making "2a+b+d" at least pi), and we can also build
a parallelogram with c = pi/2 (making "2c+b+d" at least pi).
Therefore, neither "2a+b+d" nor "2c+b+d" is inherently smaller
than pi, so that neither is inherently equal to arccos(X).

===

Suggestion: Give your angles "d" and "c" the names "x" and
"y" (if not "a-prime" and "b-prime"), respectively. The
alphabetic-pair nature of these labels more clearly conveys
the mirror-image arrangement of the angles, and it
improves the comprehensibility of equations such as your
Property 2. (Less glancing back at the diagram to remember
which angle was "c".)

===

Related Nitpick: Justifying your variable exchanges because
of rotations and reflections in the diagram --unless you
put the terms in quotation marks or something to indicate
that you don't mean them literally-- isn't really appropriate,
because the parallelogram shown is not actually symmetric
with respect to the transformations you cite.

Note that with convenient labeling --'x' for 'd' and 'y' for
'c'-- then the exchanges 'a <-> x' and 'b <-> y' seem more
natural in the equations, and less obscure in the picture,
virtually eliminating the need to explain the exchanges at
any length.

===

Nitpick: Your "Solution"s should really be called something
along the lines of "Case"s, since each addresses a distinct
variant of the problem.


Regards,

DayLateDon

[f1000]

Originally Posted by DayLateDon

In Solution 1a, the following equations (the first one is yours)

Eq1: cos( 2c+b+d ) = cos(b+d) - 2 sin(b) sin(d)
Eq2: cos( 2a+b+d ) = cos(b+d) - 2 sin(b) sin(d)

are simultaneously true. To see why, recall a+b+c+d = pi,
and manipulate as follows:

cos( 2c+b+d ) = cos( 2pi - (2c+b+d) )
= cos( 2(a+b+c+d) - (2c+b+d) )
= cos( 2a+b+d )

If "arccos-ing" both sides were legal, then one consequence
of applying that process to Eq1 and Eq2 would be that "a"
always equals "c". (Likewise, via a separate pair of
substitutions, "b" always equals "d".) Clearly, this is not
true.

Good catch! Since Matt seemed to have set up his initial equations correctly, I had assumed that the rest was just shake and bake.

I also like your recommendation on using primed variables.

Would you mind double-checking my proof as well? As you can see, cases {a, c} and {b, d} lack the elegance of my other four cases. While it's easy to calculate the roots of tan(θ), the resulting solutions for θ are far from compact.

[f1000]

Originally Posted by Ghoser777

Of course its true - given b and d, there are two interchangeable solutions for a and c. What that means is, if you have a parallelogram with a given b and d, and c comes out to be 30 and a comes out to be 50, then there exists another parallelogram with the same b and d values where a is 30 and c is 50. If you have GSP, you can convince yourself of this fact fairly quickly.

Sorry Ghoser, but you're right. It took me awhile to see it last night.

[f1000]

Typo:

Solution 2b: If a and d are given, this is actually symmetric to when a and c are given.

Should be:

Solution 2b: If a and d are given, this is actually symmetric to when b and c are given.

[DayLateDon]

Hello ...

I was called halfway across the country for over a week, so I didn't have a chance to post this in a more timely manner.

Here's my analysis of the problem:
http://www.daylateanddollarshort.com...fs/parprob.pdf

It's a bit long on exposition, but I think instructively so.

Among other things, this presentation provides a direct route to the unique solutions in four Cases, explains why those Cases have analogous solutions, illustrates why the other two Cases have ambiguous solutions, and (I hope) demonstrates how convenient labeling can help clarify analysis. (Note: I didn't triple-check the equations, so beware of any errant angle names or prime marks.)

Enjoy!
DayLateDon

[DayLateDon]

f1000 ...

I've just taken a quick glance at your solutions.

Although the underlying interpretation of the geometry may be sound, expressing the angles in terms of "atan"s and "acot"s is problematic. For one thing, the principal values of "atan" run between -pi/2 and pi/2, while the angles you want to identify are obviously in the range 0 to pi. Moreover, there's not even a universal agreement on the definition of the principal values of "acot" (see http://mathworld.wolfram.com/InverseCotangent.html), so your formulas involving this function aren't necessarily meaningful.

It's possible that your arguments need only include a disclaimer or two about the ranges you're assuming when you write "atan" and "acot", but I'd be concerned of some computational subtlety creeping in that will not be accounted for by such assumptions.

Generally, when solving for angles known to live in triangles, the best strategy is to opt for a cosine-based formulation whenever possible, since the principal-valued "acos" function has precisely the range you need and there are no ambiguous cases. (Of course, as with Matt's solutions, there are still pitfalls to avoid when dealing with angle *sums* that might fall outside the 0-to-pi range.)


Regards,
DayLateDon

[davesimondotcom]

Whew, why did I even bother to open this thread... I haven't taken a math class in 12 or 13 years and never really cared that much for it anyway.

Good thing you guys seem to know what the heck you are talking about!



This thread made a "whoosh" as it flew over my head!

[Chuckit]

I wish I knew more math. I feel really dumb reading threads like this and thinking, "Huh?"

[meelk]

Originally Posted by Chuckit

I wish I knew more math. I feel really dumb reading threads like this and thinking, "Huh?"

pffttt. this is so easy.

[f1000]

Originally Posted by DayLateDon

f1000 ...

I've just taken a quick glance at your solutions.

Although the underlying interpretation of the geometry may be sound, expressing the angles in terms of "atan"s and "acot"s is problematic. For one thing, the principal values of "atan" run between -pi/2 and pi/2, while the angles you want to identify are obviously in the range 0 to pi. Moreover, there's not even a universal agreement on the definition of the principal values of "acot" (see http://mathworld.wolfram.com/InverseCotangent.html), so your formulas involving this function aren't necessarily meaningful.

Thanks for the heads up on the ambiguity of the definition of acot. I had actually used the first definition of acot shown in that Wolfram link and had double-checked all of my calculations for both domain/range.

I had also determined some time ago, through trig identities, that my [b,c] case was identical to Ghoser's. I'll be sure to look over your own proof in the coming weeks.